【第33回数学カフェ】カメラと代数幾何学のご案内
2021年3月7日日曜日 13時から17時まで(オンライン開催)
お申し込み開始は2021年2月4日正午から
お申込サイトはこちら。https://mathcafe-33.peatix.com/view
講演者
三浦真人さん 東京大学大学院特任研究員
ご専門は Calabi—Yau 多様体、ミラー対称性、代数ビジョン、可視化、次元削減
2016年数学カフェサイエンスアゴラ出展「4次元を見てみよう」では、三浦さんの研究成果をVR機器に実装し、市民の方に体験していただきました。 当日は約4年後の進展や関連する研究についてお話して頂きます。
講演概要
射影空間は、幾何学を展開する上で、とても自然な対象です。射影空間を舞台とする幾何学は射影幾何学(projective geometry)と呼ばれ、その出自は少なくとも 15, 16 世紀に活躍した芸術家らによる透視図法の研究にまで遡る、古い学問であります。当時はすでに、ピンホールカメラなどの様々な光学装置が、デッサンの場で活用される技術となっていました。その研究は、現代では代数幾何学(algebraic geometry)として、装いを一変するほどに大きく発展しています。
一方、20 世紀後半にはカメラで撮影した画像から 3D 形状を再構成するアルゴリズムが盛んに研究されました。とくに同一の被写体を撮影した複数の画像から被写体の 3D 形状を再構成するという問題は奥が深く、その理論的側面は、多視点幾何学(multiple view geometry)と呼ばれるコンピュータ・ビジョンの一分野を築くに至りました。多視点幾何学の問題の一部は、19 世紀の射影幾何学においても考えられていましたが、80 年代、90 年代の計算機科学者らの研究によって、改めて大きな発展を遂げることになったのです。
多視点幾何学で扱うカメラの最も単純な数理モデルであるピンホールカメラ模型は、代数幾何学の言葉でいうと、射影空間における射影に他なりません。射影空間における射影は、代数多様体の間の有理写像(rational map)の典型的な例であり、代数幾何学のより高度なアイデアに触れる上でも良い出発点になります。そこで今回は、多視点幾何学における再構成問題を題材とし、射影空間や、射影空間における射影がどのようにコンピュータ・ビジョンの文脈に現れてくるのかを説明すると共に、関連する代数幾何学の入門的なトピックについてお話をします。とくに、多面体を用いて易しく記述できるトーリック多様体(toric variety)という代数多様体を例にとり、再構成問題がどのように代数幾何学的に記述されるのかを見ていきます。
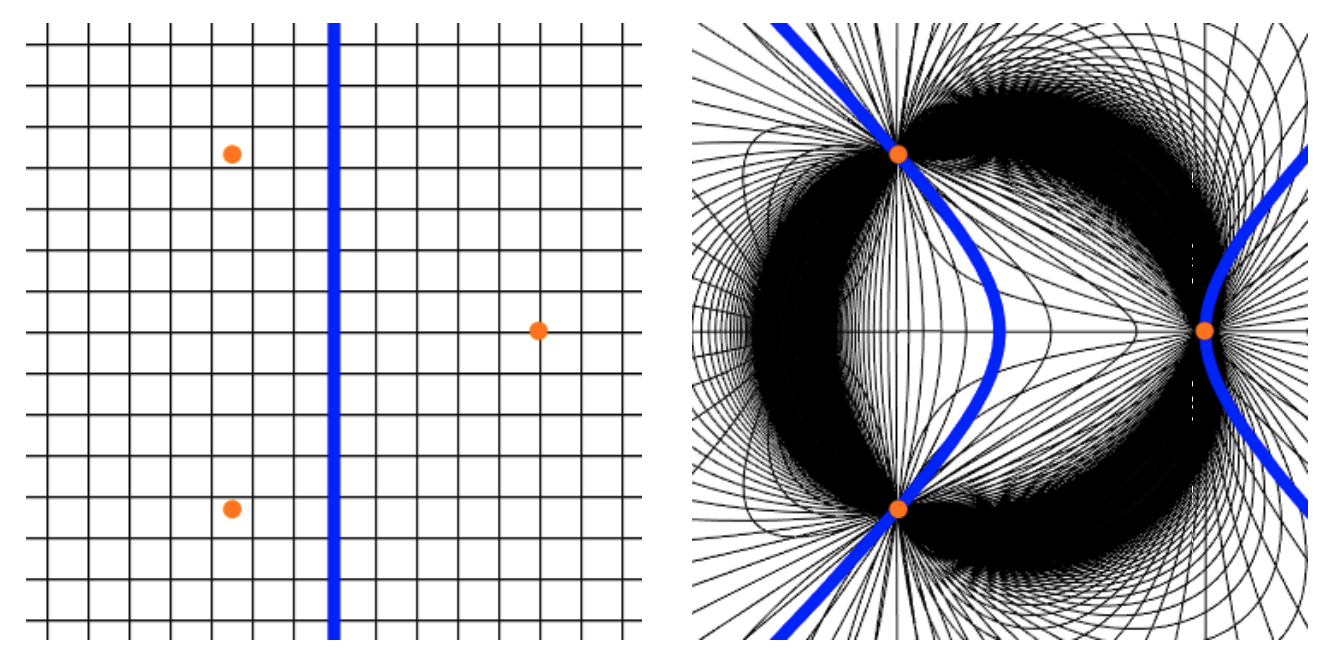
図 1 三つ目の平面人は、2 つの世界を区別できない?
サイエンスアゴラ企画の記録より
三浦さんが高次元の可視化に取り組む理由
こちらぜひご一読ください。
http://blog.miurror.net/mathcafe4d-1/
小平邦彦先生の怠け数学者の記より
数学を理解するということは、その数学的現象を「見る」ことである。「見る」というのは勿論目で見るのとは異なるが、ある種の感覚によって知覚することである。私はかつてこの感覚を「数覚」と名付けたことがある。
将来人類が進化して数覚が発達した暁には、現在われわれが苦心して証明している定理が数覚によって一目瞭然証明なしに分るようになるのではなかろうか?
という一節を引用し、高次元の可視化が数学の世界に与えうる貢献について書かれています。
仕事で高次元データを扱う人の観点から
https://qiita.com/delta2323_/items/3f9cb374efce1d97d85f
実装するときの技術的な課題について
https://qiita.com/outlandkarasu@github/items/0a1617a9bb8073fa8e40
その他以前の出展の記録は以下から見ることができます。ぜひご覧くださいませ。
https://qiita.com/advent-calendar/2016/mathcafe4d
予習用の参考文献
射影空間の間の有理写像について
川又雄二郎「射影空間の幾何学」2章, 4.1–4.3節など
Computer vision にご興味ある方向けの参考文献
Multiple View Geometry in Computer Vision
第一回予習会のご案内
2月20日17時からZoomにて開催
https://33-prep-1.peatix.com/view
主催者より
サイエンスアゴラに出展して以来4年の間にVR機器は更に社会に浸透してきました。
研究者の尽力と社会の側が常に新しい研究成果に触れ続ける努力によってテクノロジーの進化は加速していくと思います。数学カフェはその地道な積み重ねのお手伝いをしていきたいです。


[…] 第33回数学カフェのご案内 第33回数学カフェ予習会のご案内 […]
[…] 2021年2月20日17時から19時まで 【第33回数学カフェ】カメラと代数幾何学の予習会を行いました。 […]
[…] 2021年2月27日17時から19時まで 【第33回数学カフェ】カメラと代数幾何学の予習会の第2回を行いました。 […]