こんにちは。数学カフェ主催者の根上です。
数学カフェの法人化をするにあたってロゴを新しくしましたので今日は数学カフェのロゴのご紹介をしたいと思います。
今後微調整があるかもしれませんが今後のビジョンや数学としての面白さを両立できるように色々考えて作りましたのでご紹介させて下さい。
数学カフェのロゴはこちら

数学カフェのロゴに込めた要素と背景
数学カフェのロゴには
多様性あるコミュニティ
カフェ的な要素
すべての人の間のつながり
を込めています。順番にお話させて下さい。
多様性を色で表現
まず第一に表現したかったのは「多様性」です。
私は参加してくださった方から、よく
「主催者が女性だから参加しやすい雰囲気がある」
と言っていただくことがあります。
※恐らくそれはただ女性であるということが理由ではなく
様々なハードルを感じたからこそ得られた知見を反映させたいと意識してきたからだと思います。
女性というある1つのマイノリティ属性を持つために男女という分類に注目が行きがちですが
数学を学ぶ際にはもちろんそれ以外にも様々な課題がありえます。
たとえば、生物学的な男女の分類を当たり前のものとせず
LGBTQ+の方々のような多様な性指向・性自認のあり方があるのだと常に心に留めたいです。
一度にすべての課題を解決することは難しくとも
数学を学ぶ上での様々なハードルを解決していく場にしたいと考えていますし
そのために、他の運営メンバーとも共に話し合いを重ねています。
そんなわけで、ロゴは、様々な人が集まる場所を表現するためにカラフルな7つの色を採り入れました。
皆様はLGBT(注)を表すシンボル、レインボーフラッグをご存知でしょうか?
元々は、ピンク、赤、橙、黄、緑、ターコイズ、藍、紫の8色からなるものだそうで
現在はピンクとターコイズを除いた6色で構成されています。
参考:スーパーアライへの道 レインボーフラッグ&レインボーグッズ特集
数学カフェのロゴを構成する色は性的マイノリティのアライとして寄り添いたい気持ちと
様々な分野の人達が集まるコミュニティでありたいという思いを込めて
このレインボーフラッグの色を採り入れました。
レインボーフラッグとは並び順や色調が異なっているのは
色覚障害のある方でも同じ色のブロック同士を識別出来るように調節したためです。
(赤と緑は判別しにくいということもあり、赤をピンク寄りに、緑をターコイズ寄りにしました。)
ロゴを1つの大きな四角形の上に14個の四角形が乗っているとみなしたとき、
大きな四角形の対辺側に同じ色の四角形が乗っているように配置しました。
(理由はまたのちほど。)

レインボーフラッグは6色からなりますが、数学カフェのロゴはさらに白を加えた7色になっています。
レインボーマーチ札幌はLGBTを象徴するレインボーフラッグの6色に加え
「HIV/AIDS、及びゲイバッシングなどによる暴力で亡くなった方への追悼」と「現在さまざまな苦しみと闘う仲間との共生のしるし」
として白を加えた7色のフラッグを用いています。
http://rmsf.seesaa.net/article/331553435.html
このような背景から、数学カフェのロゴには戦う仲間との共生のしるしの意味も込め、7つ目の色として白を採り入れました。
ロゴ制作の基本は「使う色を少なく識別しやすいようにする」なのですが
多様な背景の人の集まる場所作りの実践の難しさも含めてロゴとして表現したいなぁという思いで作ってみました。
注:LGBTの象徴としてのレインボーフラッグ以外にも様々な性的マイノリティの象徴となるフラッグがあります。
https://lgbt-life.com/topics/LGBTsFlag/
私も勉強中の事柄なので、もし誤りがありましたら教えて頂けますと幸いです。
カフェの要素を織り込む
続いて織り込みたいと思ったものは、「カフェ感」です。
名前が「数学カフェ」なのに、ロゴにはカフェ感が醸し出されていません。
どこにカフェ要素があるのだろうか…と思われる方も多いかもしれないですね。
実は数学的な背景が背後にあります。
カフェ感のあるもの、と言ったら取っ手のついたコーヒーカップが定番でしょうか?
実は数学的にはこのコーヒーカップ(の表面)はトーラスといって
ドーナツのような3次元的な穴(数学の用語で種数といいます)を1つもつ図形に分類されます。

この下の図のように
ロゴの同じ色のブロック同士を重ね合わせると
ドーナツのような図形が出来上がります。
操作1

操作1で出来たもの(絵が下手くそですみません…)

操作2

操作2で出来たもの

こんな風にしてこっそりとロゴにコーヒーカップ的要素を織り込んでみました。
つながりを表現
数学カフェは講演会を実施するだけではなく
数学を愛好する人たちの間の繋がりを作る場でもありたいと考えています。
人同士の繋がりを表す数学的な概念として「グラフ」があります。
グラフという言葉は色々な意味を持ちえますが、
ここでは、点と、2つの点同士を結ぶ辺からなる図形のこととします。
無限に沢山のパターンがありうるグラフですが、
その性質を分類する1つの方法があります。
それは、辺同士が交わらないように曲面に埋め込み、
そのような埋め込みができる一番単純な曲面(※種数が最も小さいもの)の種類で分類する方法です。
たとえば、点が2つのグラフは、辺の数がいくつであっても
平面や球(種数が0の曲面)に埋め込むことが出来ます。
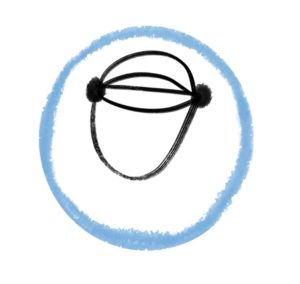
点が5つあり、また、どの2点の間にも辺があるようなグラフは
球には埋め込めませんが
(最後の1つの辺を書き込もうとすると交わってしまう。)
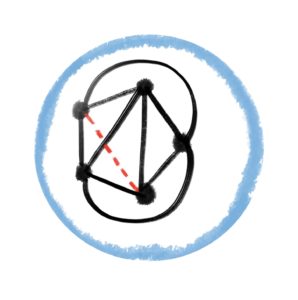
種数 1 の曲面、トーラスに埋め込むことができます。

このようにしてグラフの性質を分類することが出来ます。
さて、上で挙げた、どの2点の間にも必ず辺があるようなグラフは「完全グラフ」と言います。
3個以上の点からなる完全グラフが埋め込める曲面の最小の種数 g は
g = (n^2 − 7n + 23)/12
の小数点以下を切り捨てた数になります。
上で挙げた n = 5 の場合は、
(5×5 – 7×5 + 23) = 1.083333333…
の小数点以下を切り捨てて、種数 1 の曲面、すなわちトーラスに埋め込めることが確認できます。
そしてこの結果から、n = 7 点の完全グラフはトーラスに埋め込める最大の完全グラフとわかります。
さらに、7つの点からなる完全グラフは種数 1 の曲面(トーラス)に埋め込むと
辺によって分けられる領域をすべて三角形(辺 3 つで分けられる領域)にすることが出来ます。
数学カフェのロゴにあるカラフルな四角いブロックの同じ色どうしを重ね合わせるとトーラスになり
各ブロックを点とみなして、下図のように線を引くと
7点からなる完全グラフのトーラスへの埋め込みになります。

ご興味を持たれた方は、更に詳しく解説が載っていますのでこちらの資料を御覧ください。
終わりに
今日は数学カフェのロゴの背景をお話いたしました。
組織の目指す理想に近づけていくことこそが非常に難しく
既に多くの人が挑戦されていることだと思うので、
理想を掲げて満足するのではなく精進したいと思います。
ロゴもお手製なのでプロには及ばないのですが、考えたことをまとめるのも大事かなと思いまして書いてみました。
ここまで読んで頂きありがとうございました。
これからもどうぞよろしくお願いいたします。
